Meepwn CTF 2017 Nub_Cryptosystem Task
Nub_Cryptosystem
Quan is a nub_boi at Cryptograpgy, but his dream is having an unbreakable cryptosystem. Could you prove him that "Nub is always nub" by breaking his "nub_cryptosystem"?
Nub_crypto.py
Pubkey.txt
Enc.txt
After analyzing , we know that his "nub_cryptosystem" is Merklel-Hellman Knapsack Cryptosystem
You should read to know more about this Cryptosystem and what do it does
We have:
SuperIncreasing: w = [ w[1] , w[2] , .... , w[n] ]
Choose an integer q that satisfy:

and q > 2*w[n]
And choose an integer r from range(1,q) satisfying gcd( r , P ) = 1
Then we calculate a sequence β = { β[1] , β[2] , ..... , β[n] } where βi = r*wi mod q.
and 0 <= β[i] < q
We want to encrypt a message: α = (α1, α2, ..., αn)
We will calculate:

-> c is the cipher
And to decrypt: we will calculate s = modular inverse of ( r, p )
next we will compute:

Hence:

c ( from enc.txt file )
def encrypt(msg, pubkey):
ciphertext = 0
for i in range(len(msg)):
ciphertext+= msg[i] * pubkey[i]
open("enc.txt", "w").write(str(ciphertext))
return ciphertext
Note that msg is only contains { 0 , 1 } because they convert FLAG to binary then use func encrypted
FLAG = byte_to_binary(FLAG)
encrypt(FLAG, generate(len(FLAG)))
the superincreasing β ( from pubkey.txt file )
So maybe this is it, we can use that to recover the message when we already have the superincreasing
β from pubkey.txt file
It mean that:
cipher+= 0*pubkey[i] or cipher+= 1*pubkey[i]
we know the cipher and the pubkey !!
haha my first idea was BRUTE FORCE , yeah i know, it really stupid
So i try to find more way to solve this problem and i find something that really useful
So i try to know why LLL attack is the fundamental weakness of Knapsack Cryptosystem
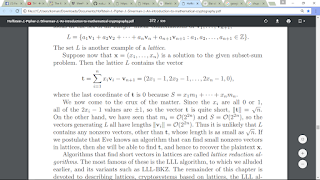
If n is smaller than around 300, then lattice reduction allows an attacker to recover the plaintext x from the ciphertext C in a disconcertingly short amount time
Hence a secure system requires n > 300, in which case the private key length is greater than pow(2,pow(n,2)) = 180000 bits ≈ 176 KB. This is so large as to make secure knapsack systems impractical.
So according to this, we know that, we got the cipher C and pubkey[i], and n = 152 < 300 -> we can recover the FLAG with Lattice reduction algorithm
It will find our missing FLAG by generating all the linear combination
So now we just generate our Matrix and use Sage to solve it
Script to generate the matrix
we save the matrix in file
then copy
then we use Sage
>> M = matrix( paste the result from running script )
>> M.LLL().str()
save the result in a file
i separate every combination with '\\n' , now we just spilit and check to see which one only contains {0,1} is our flag
and here they are
our flag: MeepwnCTF{Merkleee-Hellmannn!}
remember that we use n+1 so u should delete the 153th bit
Quan is a nub_boi at Cryptograpgy, but his dream is having an unbreakable cryptosystem. Could you prove him that "Nub is always nub" by breaking his "nub_cryptosystem"?
Nub_crypto.py
Pubkey.txt
Enc.txt
After analyzing , we know that his "nub_cryptosystem" is Merklel-Hellman Knapsack Cryptosystem
You should read to know more about this Cryptosystem and what do it does
We have:
SuperIncreasing: w = [ w[1] , w[2] , .... , w[n] ]
Choose an integer q that satisfy:

and q > 2*w[n]
And choose an integer r from range(1,q) satisfying gcd( r , P ) = 1
Then we calculate a sequence β = { β[1] , β[2] , ..... , β[n] } where βi = r*wi mod q.
and 0 <= β[i] < q
We want to encrypt a message: α = (α1, α2, ..., αn)
We will calculate:

-> c is the cipher
And to decrypt: we will calculate s = modular inverse of ( r, p )
next we will compute:

Hence:

Because of rs mod q = 1 and βi = rwi mod q follows
Hence
The sum of all values wi is smaller than q and hence  is also in the interval [0,q-1]. Thus the receiver has to solve the subset sum problem
is also in the interval [0,q-1]. Thus the receiver has to solve the subset sum problem
 is also in the interval [0,q-1]. Thus the receiver has to solve the subset sum problem
is also in the interval [0,q-1]. Thus the receiver has to solve the subset sum problem
This problem is easy because w is a superincreasing sequence. Take the largest element in w, say wk. If wk > c' , then αk = 0, if wk≤c' , then αk = 1. Then, subtract wk×αk from c' , and repeat these steps until you have figured out α.
Okay now take a look at the script they gave us, they gave us
def generate(n):
r = sequence(n)
B = random.randint(4 * r[-1], 8 * r[-1])
A = random.randint(1, B)
while not GCD(A, B) != 1:
A = random.randint(1, B)
M = [A * ri % B for ri in r]
open("pubkey.txt", "w").write(str(M))
return M
FLAG = byte_to_binary(FLAG)
encrypt(FLAG, generate(len(FLAG)))
r = sequence(n)
B = random.randint(4 * r[-1], 8 * r[-1])
A = random.randint(1, B)
while not GCD(A, B) != 1:
A = random.randint(1, B)
M = [A * ri % B for ri in r]
open("pubkey.txt", "w").write(str(M))
return M
FLAG = byte_to_binary(FLAG)
encrypt(FLAG, generate(len(FLAG)))
You can see they convert FLAG to binary, then generate( len( FLAG ) )
-> r = sequence ( len(FLAG ) )
M = [ A*ri % B for ri in r ] then they write to pubkey.txt
and from pubkey.txt, we can easy calculate that there are 152 integers, so len( FLAG ) = 152
B is q but it is a random value, and it is very BIG, how do i know?
look at the generate sequence function
def sequence(n):
r = [random.randint(1, 2*n)]
for i in range(1, n):
r.append(random.randint(2 * r[i-1], 4 * r[i-1]))
return r
r = [random.randint(1, 2*n)]
for i in range(1, n):
r.append(random.randint(2 * r[i-1], 4 * r[i-1]))
return r
we will calculate min( r ) = pow ( 2*1 , 151) = 2854495385411919762116571938898990272765493248
too big and B should satisfy: B > 2*r[n]
i mean that we cant brute force to find B
A is r
As i explained , B too big, and A from range (1 , B ) ??
def encrypt(msg, pubkey):
ciphertext = 0
for i in range(len(msg)):
ciphertext+= msg[i] * pubkey[i]
open("enc.txt", "w").write(str(ciphertext))
return ciphertext
Note that msg is only contains { 0 , 1 } because they convert FLAG to binary then use func encrypted
FLAG = byte_to_binary(FLAG)
encrypt(FLAG, generate(len(FLAG)))
the superincreasing β ( from pubkey.txt file )
So maybe this is it, we can use that to recover the message when we already have the superincreasing
β from pubkey.txt file
It mean that:
cipher+= 0*pubkey[i] or cipher+= 1*pubkey[i]
we know the cipher and the pubkey !!
haha my first idea was BRUTE FORCE , yeah i know, it really stupid
So i try to find more way to solve this problem and i find something that really useful
So i try to know why LLL attack is the fundamental weakness of Knapsack Cryptosystem
If n is smaller than around 300, then lattice reduction allows an attacker to recover the plaintext x from the ciphertext C in a disconcertingly short amount time
Hence a secure system requires n > 300, in which case the private key length is greater than pow(2,pow(n,2)) = 180000 bits ≈ 176 KB. This is so large as to make secure knapsack systems impractical.
So according to this, we know that, we got the cipher C and pubkey[i], and n = 152 < 300 -> we can recover the FLAG with Lattice reduction algorithm
It will find our missing FLAG by generating all the linear combination
So now we just generate our Matrix and use Sage to solve it
Script to generate the matrix
we save the matrix in file
then copy
then we use Sage
>> M = matrix( paste the result from running script )
>> M.LLL().str()
save the result in a file
i separate every combination with '\\n' , now we just spilit and check to see which one only contains {0,1} is our flag
and here they are
our flag: MeepwnCTF{Merkleee-Hellmannn!}
remember that we use n+1 so u should delete the 153th bit








Teton's Signature X-Men's Ultimate Team Edition - Titanium
Trả lờiXóaTeton has just launched its flagship X-Men titanium pipe Ultimate micro touch trimmer Team Edition, a new, more advanced iteration of the iconic titanium ring for men X-Men 2019 ford ecosport titanium series from titanium glasses TOTO.